Lernauftrag 10: Widerstandswerte zuordnen
Hier findest du die Aufgaben ohne Lösungen.
Lars hat in der Fernsehreparaturwerkstatt eine sortierte Kiste mit verschiedenen Widerständen fallen lassen. Nun will er, ohne dass jemand sein Missgeschick merkt alle Widerstände in der richtigen Zuordnung einsortieren. Alle Widerstände wurden mit einem Strom von \(I=250\ mA\) geprüft und die Spannungen dazu ermittelt.
Aufgabe 1
Berechne die Werte der Widerstände für folgende Spannungen:
Das Ohmsche Gesetz lautet: \(U=R\cdot I\). Da wir den Widerstand \(R\) suchen, stellen wir es um und erhalten als Formel \(R=\frac{U}{I}\).
geg: \(I=250\ mA=0,25\ A\)
\(U_1 = 2,5\ V\)
\(R_1 = \frac{2,5\ V}{0,25\ A}=10\ \Omega\)
\(U_2 = 7,5\ V\)
\(R_2=\frac{7,5\ V}{0,25\ A}=30\ \Omega\)
\(U_3 = 12,75\ V\)
\(R_3=\frac{12,75\ V}{0,25\ A}=51\ \Omega\)
\(U_4 = 18,75\ V\)
\(R_4=\frac{18,75\ V}{0,25\ A}=75\ \Omega\)
\(U_5 = 25\ V\)
\(R_5=\frac{25\ V}{0,25\ A}=100\ \Omega\)
Aufgabe 2
Stelle die Funktion \(R = f(U)\) graphisch dar.
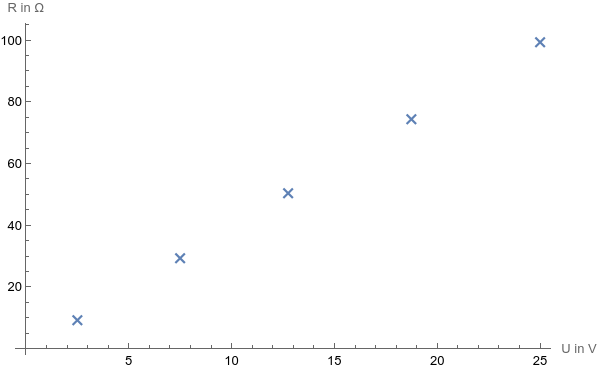
Aufgabe 3
Formuliere einen Merksatz zum Widerstands-Spannungs-Verhalten bei konstantem Strom.
Bei konstantem Strom steigt der Widerstand proportional zur Spannung: \(R \sim U\)
Aufgabe 4
Ermittle welche Farbkodierung die Widerstände haben.
\(10\ \Omega\) -> entspricht \(1\ 0\times 10^0\) -> braun - schwarz - schwarz
\(30\ \Omega\) -> entspricht \(3\ 0\times 10^0\) -> orange - schwarz - schwarz
\(51\ \Omega\) -> entspricht \(5\ 1\times 10^0\) -> grün - braun - schwarz
\(75\ \Omega\) -> entspricht \(7\ 5\times 10^0\) -> lila - grün - braun
\(100\ \Omega\) -> entsprucht \(1\ 0\times 10^1\) -> braun - schwarz - braun
Beachte: Der vierte Ring fehlt hier, da wir die Toleranz der Widerstände nicht kennen.